I had a letter in the post today. It said 'Gas Bill'.
It sounds a tempting offer. - Alan Cox
Open-loop control of absolutely unstable domains
The existence of an absolute instability is usually associated with a robust
intrinsic behaviour, largely insensitive to external noise. However, it has been
found that a well designed external harmonic forcing can have a dramatic effect, even at
exponentially small amplitudes, leading to entirely different global dynamics.
Spatially varying systems with a central absolutely unstable region are known
to give rise to self-sustained finite-amplitude globally synchronized
structures. Here it is shown how such an intrinsic behaviour
may be controlled by small-amplitude forcing applied upstream of the fully
developed oscillations. This technique allows the tuning of the frequency of the
entire system to any frequency in a wide range,
exspending only an exponentially small power.
The system under consideration is assumed to be described by a complex scalar field
in an infinite one-dimensional spatially inhomogenous domain, governed by
the complex Ginzburg–Landau equation. The complex coefficients of this PDE
depend on a slow spatial coordinate to take into account the non-uniformity of the
system. In a typical situation of interest, the local absolute growth rate displays
a single maximum and the medium is stable at infinity.
Signalling problem
In a situation where no absolutely unstable region is present, the spatial response
of the system to a localized time-harmonic forcing may be obtained in terms of
WKBJ asymptotic approximations for the entire system. For small forcing amplitudes,
the spatial response is governed by linear dynamics in the vicinity of the forcing
location and the resulting complex local wavenumber branches are derived by solving
the local dispersion relation with given frequency.
For forcing applied at a convectively unstable location, there exists a range of
frequencies associated with downstream growth. The downstream spatial response then
exponentially grows to reach finite amplitude levels. Nonlinear saturation prevents
further growth and leads to a nonlinear wavetrain at the forcing frequency,
governed by the local nonlinear dispersion relation. The
nonlinear saturation station depends, among others, on the forcing amplitude.
Further downstream, the spatial response again exponentially decays since the system
is assumed to be stable near infinity.
Self-sustained behaviour
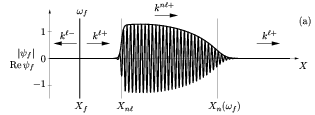
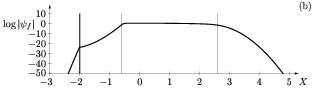
In a situation displaying a finite absolutely unstable interval, a fully nonlinear
temporally periodic state is reached without external input. An 'elephant' nonlinear
structure is selected, characterized by a sharp front at the upstream boundary of
the absolutely unstable domain. This front of real frequency acts as a wavemaker, hence
tuning the entire system to a single frequency.
Open-loop control
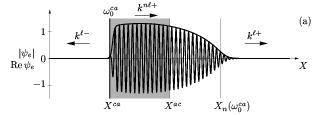
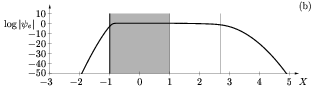
Consider now applying to the self-sustained nonlinear structure an external harmonic
forcing of small amplitude localized in the upstream convectively unstable region.
For small forcing amplitudes, both the spatial response and the self-sustained mode
are governed by linear dynamics in the neighbourhood of the forcing location.
For very weak forcing amplitudes, the spatial response does not reach a finite level
near the front of the nonlinear global mode and is thus unable to perturb the
nonlinear self-sustained waves prevailing there (fig. a).
For a critical forcing amplitude, however, the forced response reaches finite amplitude
precisely at the front and competes with the intrinsic nonlinear structure
(fig. b).
For a slightly stronger forcing, the response at the forcing frequency reaches
nonlinear saturation upstream of the front. In this regime (fig. c),
the
intrinsic oscillations are completely suppressed and replaced by the forced response
in the entire domain. For still higher forcing amplitudes, the system remains tuned
at the forcing frequency and its spatial structure does not evolve except that the
nonlinear saturation station moves usptream.
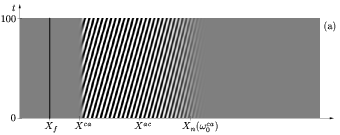
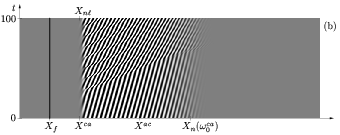
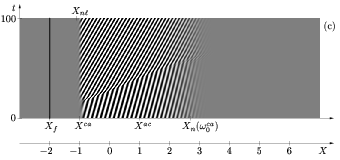
This behaviour may be interpreted as the result of two competing sources of
different frequencies at different locations: the self-sustained front
responsible for the natural nonlinear structure and the
external forcing.
In the absence of external forcing the front acts as a cornerstone
upon which the global structure is based; this front dictates its
frequency to the entire system and generates the downstream developing nonlinear
wavetrain covering the absolutely unstable region.
When forcing is applied, the intrinsic wavemaker
survives only if the upstream decaying front tail
experiences an unperturbed medium. As soon as the front is overwhelmed
by a finite-amplitude wave, the
source of the `elephant' mode is suppressed and so is the entire self-sustained
structure. The underlying absolutely unstable region plays then no role in the dynamics
since it is effectively masked by an externally imposed nonlinear wavetrain.
Thus the oscillator-type behaviour of absolutely unstable domains appears to be robust
with respect to external forcing only if the strength of the forcing does
not exceed an exponentially small level.
In summary, an externally imposed nonlinear wave
at the transition station from local convective to absolute instability
entirely suppresses the intrinsic behaviour.
Self-sustained oscillations may thus be controlled and tuned to a prescribed
frequency, chosen such as to avoid damaging resonances or to improve
performance of the system under consideration.
Due to exponential growth of the forced response in the convectively unstable
region, only an exponentially small forcing amplitude,
and hence controller power, is required to achieve this result.
[More]
Control of the rotating-disk boundary layer
[More]







