 |
Interest in this flow has been renewed by Lingwood's discovery that the nature of the impulse response changes at a critical radius: inside the critical radius perturbations are advected outwards (convective instability), whereas beyond the critical radius perturbations grow in situ (absolute instability). Moreover this critical radius closely corresponds to the station of experimentally observed turbulence onset. Previous theoretical work has established that spatially developing systems displaying an absolutely unstable region give rise to self-sustained finite-amplitude structures. The properties of the rotating-disk flow precisely meet the requirements of this theory. Thus, the present investigation has been undertaken to address the fully nonlinear régime. The objective was to analyse the naturally selected finite-amplitude state and its secondary stability properties in order to elucidate the process responsible for the sudden transition to turbulence.
Under the assumption of slow radial development of the basic flow, local saturated nonlinear wavetrains are obtained via numerical simulations of temporal evolution problems. These fully nonlinear waves take the form of spiral cross-flow vortices. Here the (1) azimuthal and (2) radial velocity components of a nonlinear saturated wave are shown over two wavelengths: (a) isolines of perturbation velocity fields,u (b) isolines of total velocity fields, (c) comparison of basic (thin lines) and total (thick lines) velocity profiles.
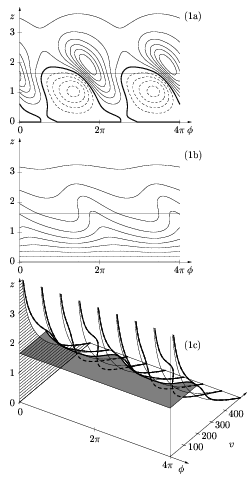
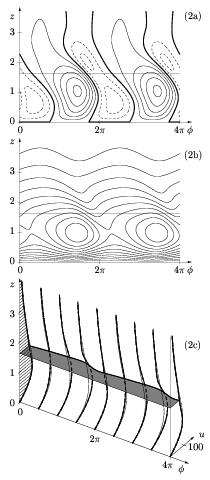
These profiles display several inflection points in both velocity components. It is thus very likely that these saturated crossflow vortices are unstable with respect to secondary perturbations. A multiple-scales analysis then consistently yields the global solution made up of these local linear and nonlinear wavetrains.
As demonstrated in earlier investigations, spatially developing systems display a nonlinear self-sustained state whenever a region of absolute instability is present. These finite-amplitude solutions (also called elephant global modes) are characterized by a stationary front located at the upstream transition from local convective to absolute instability. The selection mechanism is the following: in the absolutely unstable region amplified perturbations develop and their envelope advances upstream against the basic flow. At the station of neutral absolute instability a balance between upstream perturbation growth and downstream advection is reached and perturbations pile up at that location. Nonlinearities lead to saturation of the fluctuating amplitude and a stationary front is formed. This front generates a downstream propagating fully nonlinear wavetrain and an upstream exponentially decaying tail. It thus connects linear and nonlinear regions, acts as a source and effectively tunes the entire system to its frequency. In the present configuration, the self-sustained global solution displays the following spatial structure, where the outer region is convered by nonlinear saturated outward-spiralling cross-flow vortices while an exponentially decaying tail covers the inner region.
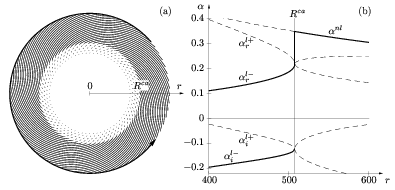
Linear secondary stability of the primary crossflow vortices is governed by Floquet theory. The numerical resolution of the associated eigenproblems yields the complete local secondary dispersion relation.
Whether or not the primary finite-amplitude waves are permanently affected by secondary disturbances depends on the absolute or convective nature of the secondary instability. Indeed, for convectively unstable secondary instabilities, an external impulse may only trigger a transient perturbation that is eventually carried away radially outwards. Without external noise and for a perfectly smooth rotating disk, transition can only occur because of secondary absolute instability of the naturally selected primary cross-flow vortices.
By carrying out an absolute stability analysis based on the local secondary dispersion relation, it has been found that the the saturated crossflow vortices that are naturally selected near the critical radius are absolutely unstable with respect to secondary perturbations. This strong secondary absolute instability explains why the naturally selected spiral vortices are not observed experimentally: as soon as the primary nonlinear vortices are generated near the critical radius, secondary perturbations develop in situ and are exponentially amplified and transition to turbulence immediately occurs.